This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Ali Ghanbari, Dept. of Computer Science, Iowa State University;
(2) Deepak-George Thomas, Dept. of Computer Science, Iowa State University;
(3) Muhammad Arbab Arshad, Dept. of Computer Science, Iowa State University;
(4) Hridesh Rajan, Dept. of Computer Science, Iowa State University.
Table of Links
- Abstract & Introduction
- Background
- Motivating Example
- Proposed Approach
- Supported DNN Bugs
- Evaluation
- Threats to Validity
- Related Work
- Conclusion, Acknowledgments & References
III. MOTIVATING EXAMPLE
In this section, we first describe how deepmufl helps programmers detect and fix bugs by presenting a hypothetical use case scenario and then motivate the idea behind deepmufl by describing the details of how deepmufl works, under the hood, on the example developed in the use case story.
Courtney is a recent college graduate working as a junior software engineer at an oil company, which frequently makes triangular structures, made of epoxy resin, of varying sizes to be used under the water. The company needs to predict with at least 60% confidence that a mold of a specific size will result in an epoxy triangle after it has been dried, and potentially shrunk, and it does not need to spend time on cutting and/or sanding the edges. Over time, through trial and error, the company has collected 1,000 data points of triangle edge lengths and whether or not a mold of that size resulted in a perfect triangle. Courtney’s first task is to write a program that given three positive real numbers a, b, and c, representing the edge lengths of the triangle mold, determines if the mold will result in epoxy edges that form a perfect triangle. As a first attempt, she writes the program shown in Listing 1.

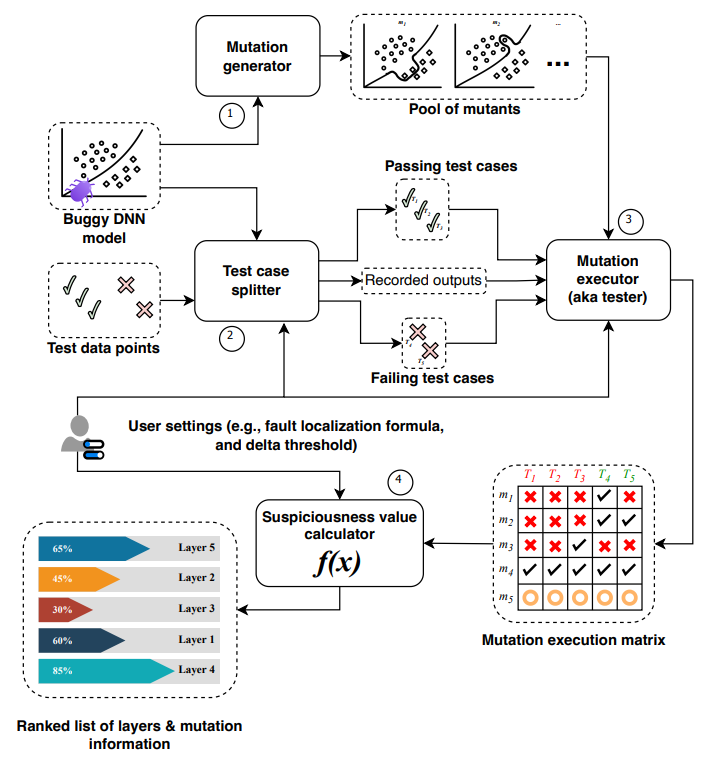
The program uses 994 out of 1,000 data points for training a model. After testing the model on the remaining 6 data points, she realizes that the model achieves no more than 33% accuracy. Fortunately, Courtney uses an IDE equipped with a modern DNN fault localization tool, named deepmufl, which is known to be effective at localizing bugs that manifest as stuck accuracy/loss. She uses deepmufl, with its default settings, i.e., Metallaxis with SBI, to find the faulty part of her program. The tool receives the fitted model in .h5 format [48] together with a set of testing data points T and returns a ranked list of model elements; layers, in this case. After Courtney provides deepmufl with the model saved in .h5 format and the 6 testing data points that she had, within a few seconds, the tool returns a list with two items, namely Layer 2 and Layer 1, corresponding to the lines 5 and 4, respectively, in Listing 1. Once she navigates to the details about Layer 2, she receives a ranked list with 5 elements, i.e., Mutant 12: replaced activation function ‘relu’ with ‘softmax’, ..., Mutant 10: divided weights by 2, Mutant 11: divided bias by 2. By seeing the description of Mutant 12, Courtney immediately recalls her machine learning class wherein they were advised that in classification tasks they should use softmax as the activation function of the last layer. She then changes the activation function of the last layer at Line 5 of Listing 1 from relu to softmax. By doing so, the model achieves an accuracy of 67% on the test dataset, and similarly on a cross-validation, exceeding the expectations of the company.

We now describe how deepmufl worked, under the hood, to detect the bug via Metallaxis’ default formula. Figure 1 depicts the structure of the model constructed and fitted in Listing 1. Each edge is annotated with its corresponding weight and the nodes are annotated with their bias values. The nodes are using ReLU as the activation function. In this model, the output T is intended to be greater than the other output if a, b, and c form a triangle, and ∼T should be greater than or equal to the other output, otherwise.
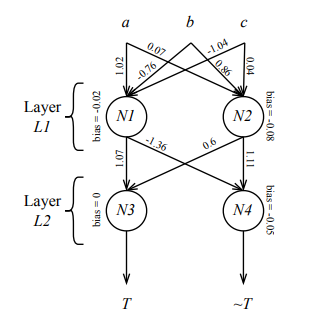
Table 1 shows an example of how deepmufl localizes the bug in the model depicted in Figure 1. In the first two columns, the table lists the two layers, and within each layer, the neurons. For each neuron three mutators are applied, i.e., halving weight values, halving bias value, and replacing the activation function. More mutators are implemented in deepmufl, but here, for the sake of simplicity, we only focus on 3 of them and also restrict ourselves to only one activation function replacement, i.e., ReLU vs. softmax.
As we saw in Courtney’s example, she had a test dataset T with 6 data points which initially resulted in 33% accuracy. These six data points are denoted T1, ..., T6 in Table 1, where correctly classified ones are colored green, whereas misclassified data points are colored rose. deepmufl generates 12 mutants for the model of Figure 1, namely, M1, ..., M12. Each mutant is a variant of the original model. For example, M1 is the same as the model depicted in Figure 1, except the weights of the incoming edges to neuron N1 are halved, i.e., 0.51, -0.38, and -0.52 from left to right, while M9 is the same as the model depicted in Figure 1, except that the activation functions for N3 and N4 are softmax instead of relu. After generating the mutants, deepmufl applies each mutant on the inputs T1, ..., T6 and compares the results to that of the original model. For each data point T1, ..., T6, if the result obtained from each mutant M1, ..., M12 is different from that of the original model, we put a bullet point in the corresponding cell. For example, two bullets points in the row for M3 indicate that the mutant misclassifies the two data points that used to be correctly classified, while other data points, i.e., T1, ..., T4, are misclassified as before. Next, deepmufl uses SBI formula [46] to calculate suspiciousness values for each mutant m ∈ {M1, ..., M12}, individually. These values are reported under the one but last column in Table 1. Lastly, deepmufl takes the maximum of the suspiciousness values of the mutants corresponding to a layer and takes it as the suspiciousness value of that layer (c.f. Eq. 1 in §II). In this particular example, layer L1 gets a suspiciousness value of 0, while L2 gets a suspiciousness value of 1. Thus, deepmufl ranks L2 before L1 for user inspection and for each layer it sorts the mutants in descending order of their suspiciousness values, so that the user will understand what change impacted most the originally correctly classified data points. In this case, M12 and M9 wind up at the top of the list, and as we saw in Courtney’s story, the information associated with the mutations helped fixing the bug.