This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Vianney Brouard, ENS de Lyon, UMPA, CNRS UMR 5669, 46 All´ee d’Italie, 69364 Lyon Cedex 07, France; E-mail: [email protected].
Table of Links
- Abstract & Introduction and presentation of the model
- Main results and biological interpretation
- First-order asymptotics of the mutant sub-populations for an infinite mono-directional grap
- First-order asymptotics of the mutant sub-populations for a general finite trait space (Theorem 2.1)
- Convergence for the stochastic exponents (Theorem 2.2)
- Acknowledgements & References
5 Convergence for the stochastic exponents (Theorem 2.2)

Using a similar approach as in step 1 of the proof of Proposition 3.1, we prove that (87) converges to 0, which gives (86
Step 2) Now we are going to prove the result of Theorem 2.2 conditioned on {W > 0}. We begin with the initial phase using the following Lemma.
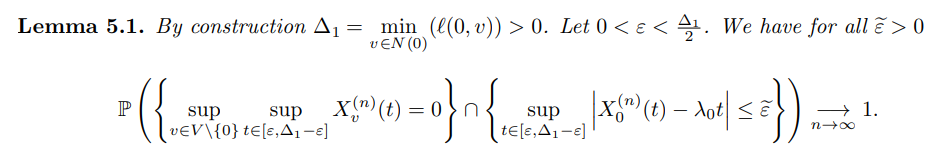
Proof. Using a similar approach as in the proof of Lemma 3.4 just by adapting the situation, one can prove that

Proof. The proof of this Lemma is obtained by adapting the one of Proposition 2 of [13] because the behavior of the models are similar between two times of change of slope. Indeed, in our case, the property of branching is satisfied, there is no interaction between individuals except mutational exchange. In [13] although there are interactions between individuals, the model is well approximated by branching populations between two changes of slope (corresponding to either a new born trait or either a change of the dominant trait) as in the present work.




