This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Vianney Brouard, ENS de Lyon, UMPA, CNRS UMR 5669, 46 All´ee d’Italie, 69364 Lyon Cedex 07, France; E-mail: [email protected].
Table of Links
- Abstract & Introduction and presentation of the model
- Main results and biological interpretation
- First-order asymptotics of the mutant sub-populations for an infinite mono-directional grap
- First-order asymptotics of the mutant sub-populations for a general finite trait space (Theorem 2.1)
- Convergence for the stochastic exponents (Theorem 2.2)
- Acknowledgements & References
4 First-order asymptotics of the mutant sub-populations for a general finite trait space (Theorem 2.1)

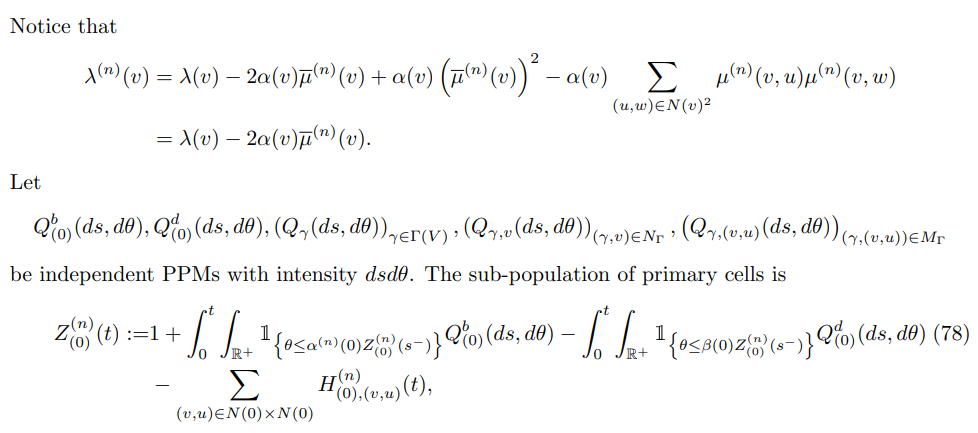
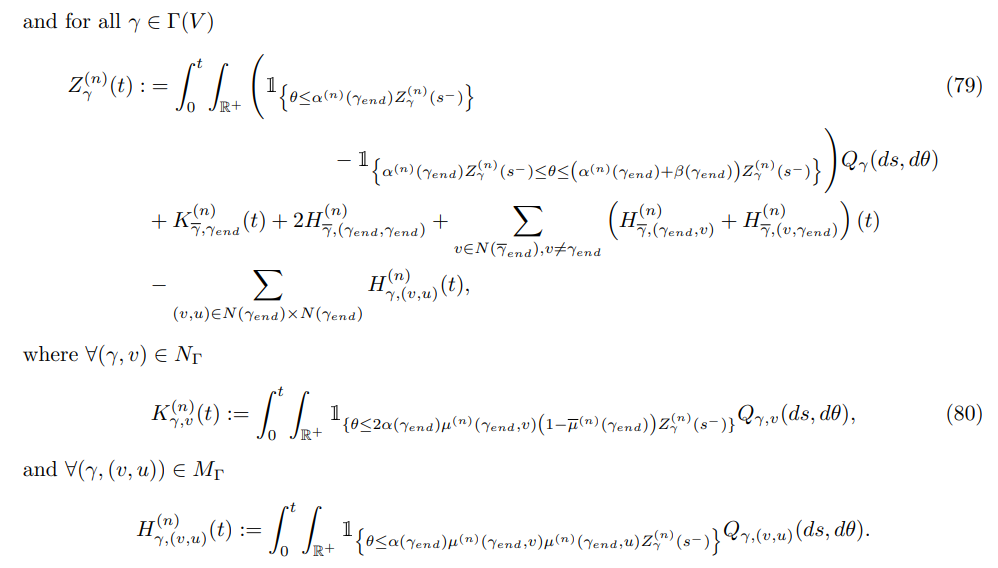

Notice that with such a construction it immediately follows the monotone coupling

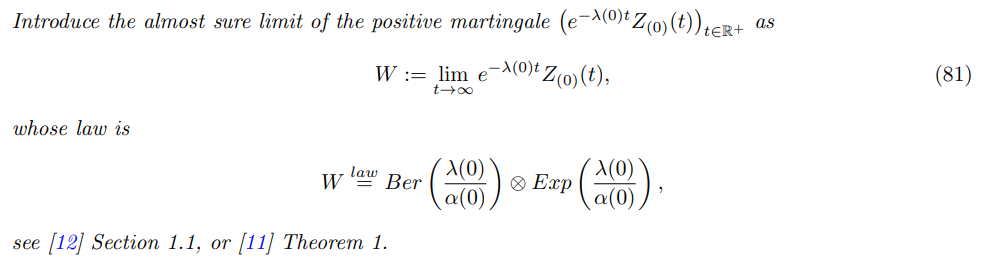

In the next definition, we are going to introduce an equivalence relation on Γ(V ). Two paths are said to be equivalent if they are the same up to cycles (in particular cycles formed by backward mutations are taken into account). More precisely, that there exists a minimal path, from which the two previous paths are using all the edges, but potentially also some other edges forming cycles. The aim of this equivalence relation is to say that among one class of equivalence, only the path with the minimal length may contribute for the asymptotic of the mutant sub-population sizes

Now we have all the preliminary results and definitions to prove Theorem 2.1.

Proof of Theorem 2.1. We show Equation (11). The proof of Equation (12) is similar and is left to the reader.


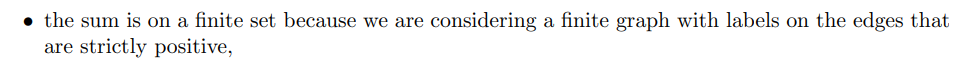
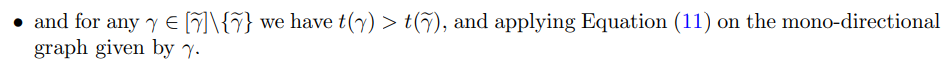
And the last term of the r.h.s converges to 0 because




