This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Vianney Brouard, ENS de Lyon, UMPA, CNRS UMR 5669, 46 All´ee d’Italie, 69364 Lyon Cedex 07, France; E-mail: [email protected].
Table of Links
- Abstract & Introduction and presentation of the model
- Main results and biological interpretation
- First-order asymptotics of the mutant sub-populations for an infinite mono-directional grap
- First-order asymptotics of the mutant sub-populations for a general finite trait space (Theorem 2.1)
- Convergence for the stochastic exponents (Theorem 2.2)
- Acknowledgements & References
Abstract
We aim at understanding the evolution of the genetic composition of cancer cell populations. To this aim, we consider a branching individual based model representing a cell population where cells divide, die and mutate along the edges of a finite directed graph (V, E). The process starts with only one cell of trait 0. Following typical parameter values in cancer cell populations we study the model under large population and power law mutation rates limit, in the sense that the mutation probabilities are parameterized by negative powers of n and the typical sizes of the population of our interest are positive powers of n. Under non-increasing growth rate condition (namely the growth rate of any sub-population is smaller than the growth rate of trait 0), we describe the time evolution of the first-order asymptotics of the size of each sub-population on the log(n) time scale, as well as in the random time scale at which the initial population, resp. the total population, reaches the size n t . In particular, such results allow to characterize whose mutational paths along the edges of the graph are actually contributing to the size order of the sub-populations. Without any condition on the growth rate, we describe the time evolution of the orders of magnitude of each sub-population. Adapting techniques from [13], we show that these converges to positive deterministic non-decreasing piecewise linear continuous functions, whose slopes are given by an algorithm.
Keywords: cancer evolution, multitype branching processes, finite graph, long time behavior, power law mutation rates, population genetics.
1 Introduction and presentation of the model




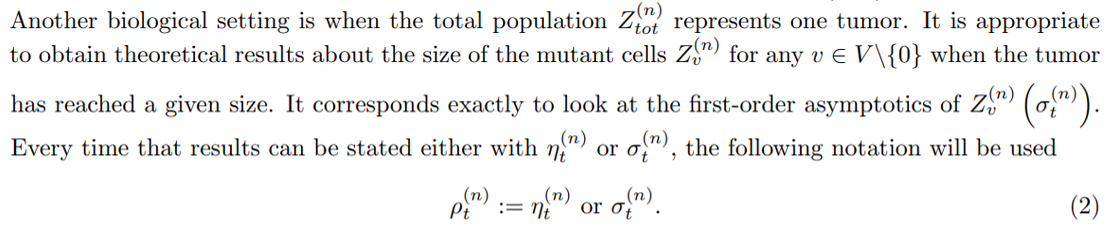
In the present work the population of cells will be studied in different time-scales: the random timescale

and the following deterministic approximation

where
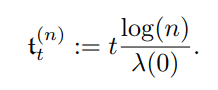

For any finite oriented labeled graph (V, E, L) under the following non-increasing growth rate condition

Without any assumption on the growth rate function λ, the study is made on the deterministic timescale of Equation (4). As in [13, 3, 5, 8, 14, 2, 30] the asymptotic behaviors are obtained on the following stochastic exponent processes
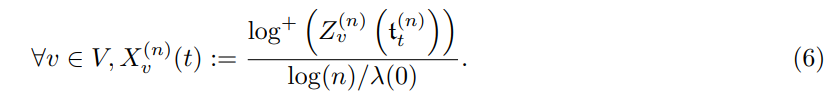
The results are presented in Theorem 2.2. It is the exponent as a power of n that is tracked for any sub-populations, whereas Theorem 2.1 gives directly the size order on n, this is a refined result. Up to our knowledge, it is the first model considering the power law mutation rates regime (1) capturing this level of refinement on the asymptotic behaviors. Two new significant results emerge.
First it shows the remarkable result that under Assumption (5) the randomness on the first-order asymptotics of any mutant sub-populations is fully given by the stochasticity of only one random variable W -encoding the randomness on the long time for the lineage of wild-type cells issued from the initial cell. It means that the stochasticity for any mutant sub-population is fully driven, at least at the first-order asymptotics, by the randomness on the growth of the wild-type population and not from the dynamics of any lineage of a mutant cell, as well as the stochastic processes generating mutations. Second it characterizes exactly whether a mutational path on the graph structure of the trait space asymptotically contributes to the growth of the mutant sub-populations. Whereas having asymptotic results on the stochastic exponents only allows to discriminate some paths and not to determine exactly whose paths are actually contributing to the asymptotic growth of the mutant sub-populations. More precisely, if the weight of a path is defined as the sum of the label of its edges, asymptotic results on the stochastic exponent gives that for every trait v, among the paths from 0 to v only those with the less weight might contribute to the asymptotic growth of trait v. On the contrary, having results directly on the first-order asymptotics of the mutant sub-populations allows to discriminate among those paths with the less weight those which actually contributes to the dynamics of trait v. In particular among those paths with the less weight only those with the maximal number of neutral mutations on their edges have an asymptotic impact on the growth of trait v. Indeed an additional multiplicative factor of order log(n) for each neutral mutation of a path is captured when looking at the first-order asymptotics and is obviously not captured with asymptotic results only on the stochastic exponents.
Moreover it is the first time that this power-law mutation rates regime is studied in the random timescale of Equation (3) up to our knowledge. From the biological point of view it is more interesting to get result on such random time-scale instead of the deterministic one. We obtain that the randomness on the first-order asymptotics of any mutant sub-populations is fully given by the stochasticity on the survival of the lineage of wild-type cells issued from the initial cell.

As in [7, 6], compared to the different models in [13, 3, 5, 8, 14, 2, 16], the initial population Z (n) (0) is not assumed to have a macroscopic size. It introduces a supplementary randomness on how the wild-type population is stochastically growing to get a macroscopic size. But contrary to [7, 6], we do not condition on the survival of the wild-type population or on the stopping times of Equation (3) to be finite.
In [28] Nicholson and Antal study a similar model under a slightly less general non-increasing growth rate condition. More precisely, in their case all the growth rates of the mutant populations are strictly smaller than the growth rate of the wild-type population: ∀v ∈ V \{0}, λ(v) < λ(0). But the main difference remains the mutation regime. In their case, only the last mutation is in the power law mutation rates regime, all other mutations have a fixed probability independent of n. In Theorem 2.1 the case where all mutations are in the power law mutation rates regime is treated. Also Nicholson and Antal are interested in obtaining the distribution of the first time that a mutant sub-population gets a mutant cell. Whereas in the present work the first-order asymptotics of the sizes of the mutant sub-populations over time are studied.
In [29] Nicholson, Cheek and Antal study the case of a mono-directional graph where the time tends first to infinity with fixed mutation probabilities. In particular they obtain the almost sure first-order asymptotics of the size of the different mutant sub-populations. Under the non-increasing growth rate condition, they are able to characterized the distribution of the limit random variables they obtained. Without any condition on the growth rates, they study the distribution of the random limit they obtained under the small mutation probabilities limit, using the hypothesis of an approximating model with less stochasticity. Notice that the mutation regime they study is not the large population power law mutation rates regime of Eq. (1) as considered in the present work. Under the latter regime both the size of the population goes to infinity and the mutation probabilities to 0, through the parameter n, see Equation (1).
In [18] Gunnarson, Leder and Zhang study a similar model as the one in the present work and are also interested in capturing the evolution over time of the genetic diversity of a population of cells, using in their case the well-known summary statistic called the site frequency spectrum (SFS). The main difference is the mutation regime because they are not considering the power law mutation rates limit. In their case the mutation probabilities are fixed. Also, they restrict the study to the neutral cancer evolution case. In particular, as in the present work, they capture the first-order asymptotics of the SFS at a fixed time and at the random time at which the population first reaches a certain size. Two noticeable similarities in the results are that the first-order asymptotics of the SFS converges to a random limit when evaluated at a fixed time and to a deterministic limit when evaluated at the stochastic previous time. One could argue that in the present work the correct convergence for the latter case is actually a stochastic limit. But the stochasticity is fully given by the survival of the initial lineage of cells of trait 0, so conditioned on such an event at the end the limit is a deterministic one. In particular the results of Gunnarson, Leder and Zhang are all conditioned on nonextinction of the population.
In [16] Gamblin and Lambert study a model of an exponentially growing asexual population that undergoes cyclic bottlenecks under the large population power law mutation rates regime. Their trait space is composed of 4 sub-populations 00, 10, 01 and 11, where two paths of mutations are possible 00 7→ 10 7→ 11 and 00 7→ 01 7→ 11. They study the special case where one mutation (10) has a high-rate but is a weakly beneficial mutation whereas the other mutation (01) has a low-rate but is a strongly beneficial mutation. In particular they show the noticeable result that due to cyclic bottlenecks only a unique evolutionary path unfolds but modifying their intensity and period implies that all paths can be explored. Their work relies on a deterministic approximation of the wild-type sub-population 00 and some parts of the analysis of the behavior of the model is only obtained due to heuristics. The present work, and more specifically Theorem 2.2 because they are considering selective mutations, can be used and adapted to consider the case of cyclic bottlenecks in order to prove rigorously their results, in the specific trait space that they consider as well as on a general finite trait space.
The rest of the paper is organised as follows. In Section 2 the results and their biological interpretations are given. Sections 3 and 4 are dedicated to prove Theorem 2.1, which assumes Equation (5). In Section 3 the mathematical definition of the model is given for an infinite mono-directional graph as well as the proof in this particular case. The generalisation of the proof from an infinite mono-directional graph to a general finite graph is given in Section 4. In Section 5, Theorem 2.2 is proved adapting results from [13].

